Question Corner and Discussion Area
Question Corner and Discussion Area
What is the square root of i?There are two square roots of i:
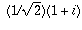 and
and 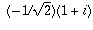 .
You can check that these are indeed square roots of i: just square
each of them, and you get i.
.
You can check that these are indeed square roots of i: just square
each of them, and you get i.
The important question is, how are these answers obtained?
An elementary, but not the best, way to obtain
this answer is to solve the equation
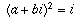 for a and b. If you expand this equation
using the rules for complex multiplication,
you get
for a and b. If you expand this equation
using the rules for complex multiplication,
you get 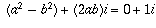 . Equating real and
imaginary parts gives
. Equating real and
imaginary parts gives 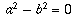 and 2ab = 1.
and 2ab = 1.
The equation 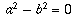 means
means 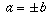 . However, if you
plug a=-b into the second equation you get
. However, if you
plug a=-b into the second equation you get 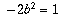 which
can not be satisfied by any real number b. Therefore, the case
a = -b is not possible, meaning a must equal b. Then the second
equation becomes
which
can not be satisfied by any real number b. Therefore, the case
a = -b is not possible, meaning a must equal b. Then the second
equation becomes 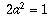 . This means either
. This means either 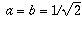 or
or 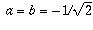 . These are the answers that were given
above.
. These are the answers that were given
above.
However, the easiest and most insightful way to take the square root of a complex number (as well as any higher order roots) is to use the geometric representation of the complex numbers. Just as we can plot real numbers as points on a line, we can think of complex numbers as lying on a plane. The horizontal (real) axis corresponds to the real part of the complex number and the vertical (imaginary) axis corresponds to the imaginary part. For example, the number 3 + 2i is located at the point (3,2) which is two units above and three units to the right of the origin.
What is most useful about this visualisation of the complex numbers is how addition and multiplication behave. To add two numbers a + bi and c + di, we can think of shifting the first one c units to the right and d units up.
Multiplication is a bit more difficult to see.
Before we go on, it is useful to introduce another means of specifying points
in the plane.
Suppose that X is any point in a plane and suppose that O is the origin.
If we know the distance r from X to the origin O and we also know
the angle 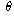 between
the positive real axis and the line segment OX, we
can locate the point X.
This angle and distance are known as the polar coordinates of X.
Multiplication corresponds to adding the angles of the two points
and multiplying their lengths.
between
the positive real axis and the line segment OX, we
can locate the point X.
This angle and distance are known as the polar coordinates of X.
Multiplication corresponds to adding the angles of the two points
and multiplying their lengths.
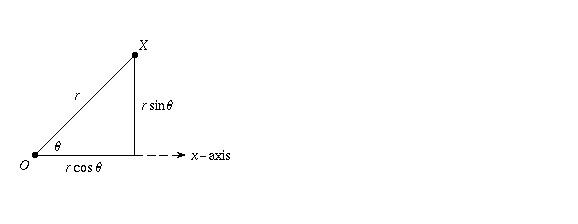
The reason for this has to do with trigonometry: the coordinates of
the point whose distance is r and whose angle is 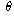 are given by
are given by
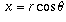 ,
, 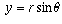 . That
means it is the complex number
. That
means it is the complex number
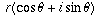 which
equals
which
equals 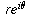 because of de Moivre's formula (which is explained
in the answer to another question). If you multiply two numbers like that, you get
because of de Moivre's formula (which is explained
in the answer to another question). If you multiply two numbers like that, you get
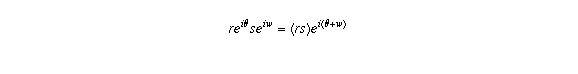
(the laws of exponents still hold for complex exponential).
In other words, the product is a complex number whose distance from
the origin is rs (the products of the distances of the factors), and
whose angle is 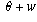 (the sum of the angles of the factors).
(the sum of the angles of the factors).
Understanding multiplication helps us understand other operations such as taking the square root. For the sake of simplicity, first consider the case in which the number we are interested in has a distance of 1 from the origin. The square root of this number also has a distance of 1 from the origin and forms an angle with the real axis which is 1/2 of the angle corresponding to the original number. In the event that the number is not 1 unit away from the origin, we obtain new distance from the origin by taking the square root of the old distance from the origin (here the lengths are positive real numbers and the notion of "square root" is already defined).
Now we can understand why we got the answer we did for the square root of i.
It is easily seen that i forms an angle of 90 degrees with the
real axis and has distance of 1 from the origin.
Its square root is the number with a distance of 1 from the origin and
an angle of 45 degrees from the real axis
(which is
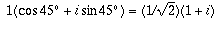 ).
).
A cautious reader will note that there is some ambiguity in choice of the angle
in our definition of polar coordinates. A point of distance 1
from the origin creating an angle of 45 degrees with the real axis is
the same point which is 1 unit from the origin and forms an angle of 405
degrees with the real axis.
Generally we always insist that the angle be between 0 and 360 degrees.
Note however that when taking the square root of a complex
number it is also important
to consider these other representations.
For instance, i can also be viewed as being 450 degrees from the origin.
Using this angle we find that the number 1 unit away from the origin and
225 degrees from the real axis
(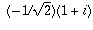 ) is also a square root of i.
) is also a square root of i.
![]() Go backward to Why is e^(pi*i) = -1?
Go backward to Why is e^(pi*i) = -1?![]() Go up to Question Corner Index
Go up to Question Corner Index![]() Go forward to What is i to the Power of i?
Go forward to What is i to the Power of i?![]() Switch to text-only version (no graphics)
Switch to text-only version (no graphics)![]() Access printed version in PostScript format (requires PostScript printer)
Access printed version in PostScript format (requires PostScript printer)![]() Go to University of Toronto Mathematics Network
Home Page
Go to University of Toronto Mathematics Network
Home Page