Table of Contents

1. Pregame: Some Highlight Footage
2. Human Accomplishments to date are spectacular!
   1. Istanbul’s Haghia Sophia
   2. A Roman Road in Pompeii
   3. Apollo 11 Moon Landing
3. Humans must confront major challenges!
   1. Human Population
   2. Climate Change
   3. Nuclear Proliferation
4. Calculus Distilled
   1. Fundamental problems leading to calculus
   2. Resolution of Slope Problem: Limit of Secant Lines onto Tangent Line
   3. Area Under a Curve as a Limit of Area of Fine Approximations by Rectangles
   4. Fundamental Theorem of Calculus
   5. Smooth Structure on Small Scales
   6. Exploded views of calculus topics
5. Inventors of Calculus
   1. Gottfried Leibniz
   2. Isaac Newton
   3. A ranking of the most influential human beings in history.
6. Motion of the Planets?
   1. Newton’s Law of Universal Gravitation
   2. Laplacian Determinism
7. Newton’s law of universal gravitation is inconsistent with the constancy of the speed of light
8. Pictures of some mathematicians working today.
9. Advertisement: Toronto Math Circles at the Fields Institute

Pregame: Some Highlight Footage ↩

• Pythagorean Theorem: $a^2 + b^2 = c^2.$

• Irrationality of the square root of 2: [$\sqrt{2} \neq \frac{p}{q}$] for whole numbers $p,q$.

• Golden Ratio

Human Accomplishments to date are spectacular! ↩

Istanbul’s Haghia Sophia ↩

• This building was designed and built in the 5th century!

A Roman Road in Pompeii ↩

• How many stones do you need to build a road that goes from Jarvis Collegiate to Bloor and Yonge? to Edmonton?

Apollo 11 Moon Landing ↩

• Humans went to the moon! Where next?

Humans must confront major challenges! ↩

Human Population ↩

Climate Change ↩

Global Warming?

Nuclear Proliferation ↩

Nuclear Test in Operations Crossroads, Bikini Atoll

Nevada Nuclear Test Site

Calculus Distilled ↩

Fundamental problems leading to calculus ↩

• Area Problem. Resolved by carefully understanding the rectangle: $\mbox{Area} = \mbox{Base} \times \mbox{Height}.$

• Slope of Curve at Point Problem: Resolved by carefully understanding the slope of a line: $\frac{\mbox{Rise}}{\mbox{Run}}$

• $\lim_{x \rightarrow c} f(x) = ?$. This is the key new spice that underpins calculus!

Resolution of Slope Problem: Limit of Secant Lines onto Tangent Line ↩

• Slope of a curve as a limit of slopes of secant lines converging to tangent line

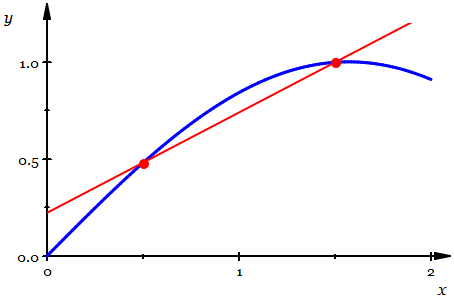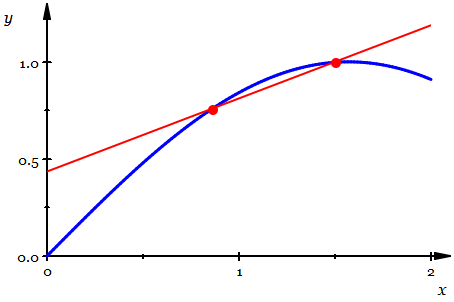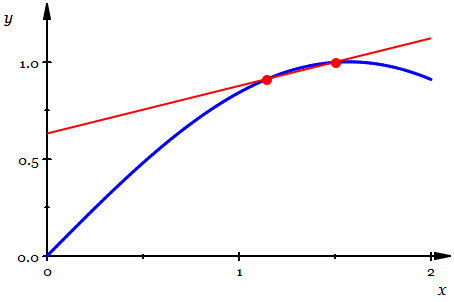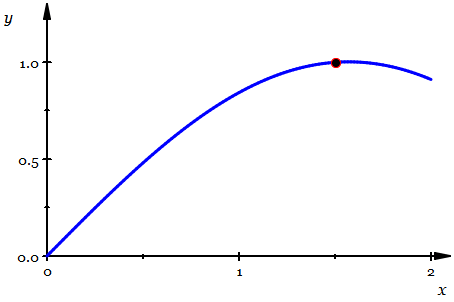
This idea leads us to define the slope of a curve as a limit of difference quotients:

$$ f’ (x) = \frac{df}{dx}(x) = \lim_{h\rightarrow 0} \frac{f(x+h) - f(x)}{(x+h) - x}.$$

Area Under a Curve as a Limit of Area of Fine Approximations by Rectangles ↩

• Area under a curve is understood as limit of areas of many shrinking width rectangles.

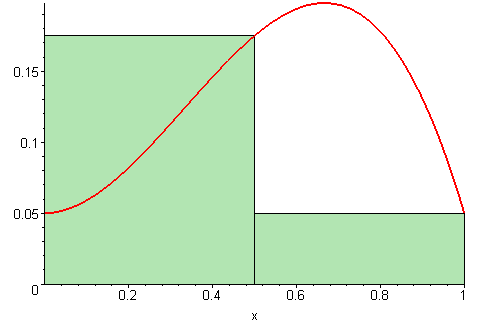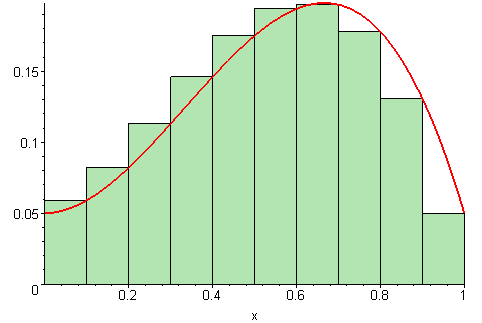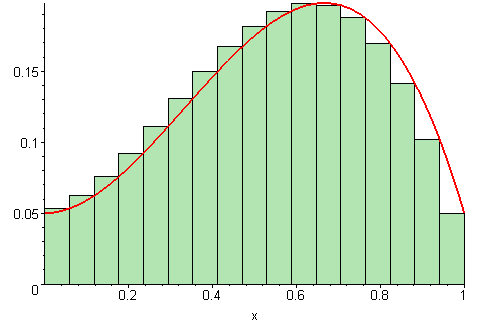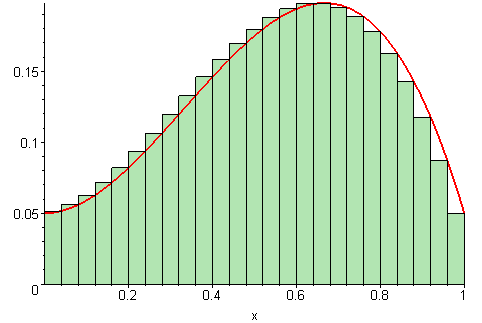
Once you see this idea, you can break up surfaces into squares:

Fundamental Theorem of Calculus ↩

This idea gives us a trick to often “add up” all the rectangles. Some chunk of the calculus class toolbox is learning different versions of applying this trick.

Smooth Structure on Small Scales ↩

Calculus: A Toolbox for studying objects which behave nicely enough on small scales.

• Determinism; Time Evolution; Idea of Rate
• Optimization
• Smooth Geometry

Exploded views of calculus topics ↩

Inventors of Calculus ↩

Gottfried Leibniz ↩

Isaac Newton ↩

Isaac Newton is the most influential scientist ever. He lived 84 years from 1643 to 1727.

• Newton is regarded as the 2nd most influential human being in history.
• 1661 Entered Trinity College, Cambridge.
• 1665 Discovered Binomial Series
• 1665 Great Plague. Cambridge shuts down. Newton discovers the keys to the universe.
• 1669 Became Lucasian Professor of Mathematics.
• 1687 Publishes Principia Mathematica.
  • Newton’s Laws of Motion
  • Newton’s Law of Universal Gravitation
• 1699-1716 Newton vs. Leibniz Calculus Controversy
• French mathematician Joseph-Louis Lagrange on Newton:

Newton was the greatest genius who ever lived, and once added that he was also “the most fortunate, for we cannot find more than once a system of the world to establish.

• Newton was rather more modest. In a letter to Robert Hooke, he wrote:

If I have seen further it is by standing on the shoulders of Giants.

(Though some historians think the above quote was an attack on Hooke who was short and hunchbacked, rather than or in addition to a statement of modesty.)

• Another Newton quote:

I do not know what I may appear to the world, but to myself I seem to have been only like a boy playing on the sea-shore, and diverting myself in now and then finding a smoother pebble or a prettier shell than ordinary, whilst the great ocean of truth lay all undiscovered before me.

A ranking of the most influential human beings in history. ↩

Hart’s Top 10 (from the 1992 edition)

1. Muhammad (c.570–632) The central human figure of Islam, regarded by Muslims as the messenger and last prophet of God. Active as a social reformer, diplomat, merchant, philosopher, orator, legislator, and military leader.
2. Isaac Newton (1643–1727) English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian. His law of universal gravitation and three laws of motion laid the groundwork for classical mechanics.
3. Jesus Christ (7–2 BC – AD 26–36) The central figure of Christianity, revered by Christians as the Son of God and the incarnation of God and regarded as a major prophet in the religion of Islam.
4. Gautama Buddha (563 BC–483 BC) Spiritual teacher and philosopher. Founder of Buddhism.
5. Confucius (551 BC–479 BC) Chinese thinker and social philosopher, whose teachings and philosophy have deeply influenced Chinese, Korean, Japanese, and Vietnamese thought and life.
6. St. Paul (5–67) One of the most notable of early Christian missionaries, credited with spreading Christianity outside of Palestine.
7. Cai Lun (50–121) Widely regarded as the inventor of paper and the papermaking process.
8. Johannes Gutenberg (1398–1468) German printer who invented the mechanical printing press.
9. Christopher Columbus (1451–1506) Italian navigator, colonizer and explorer whose voyages led to general European awareness of the American continents.
10. Albert Einstein (1879–1955) German theoretical physicist, best known for his theory of relativity and specifically mass–energy equivalence, expressed by the equation $E = mc^2$.

Historically Influential Careers:

• Religious or Philosophical Leaders: 1, 3, 4, 5, 6
• Scientists: 2, 10
• Paper and Printing Inventors: 7,8
• Explorer: 9

Motion of the Planets? ↩

Brahe’s body has recently been exhumed.

• Kepler’s Cosmological Theory (Mysterium Cosmogrphaicum)
• Kepler’s laws of planetary motion

1. The orbit of every planet is an ellipse with the Sun at a focus.
2. A line joining a planet and the Sun sweeps out equal areas during equal intervals of time.[1]
3. The square of the orbital period of a planet is directly proportional to the cube of the semi-major axis of its orbit.

Remarks:

• The Kepler Applet provides a nice visualization.
• Kepler obtained these insights by carefully studying astronomical data.

Newton’s Law of Universal Gravitation ↩

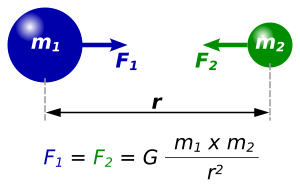
Every point mass attracts every single other point mass by a force pointing along the line intersecting both points. The force is directly proportional to the product of the two masses and inversely proportional to the square of the distance between the point masses: $$ F = G \frac{m_1 m_2}{r^2}, $$ where:

• $F$ is the magnitude of the gravitational force between the two point masses,
• $G$ is the gravitational constant,
• $m_1$ is the mass of the first point mass,
• $m_2$ is the mass of the second point mass, and
• $r$ is the distance between the two point masses.

Newton showed (and we could do it together with some preparatory work) that Kepler’s laws emerge as consequences of his universal law of gravitation.

The star S2 orbiting the black hole at the center of the Milky Way.

A more recent application of these ideas involves the orbit of stars around the galactic center of the Milky Way.

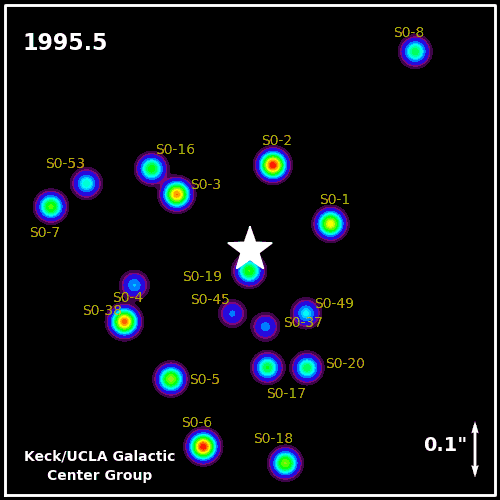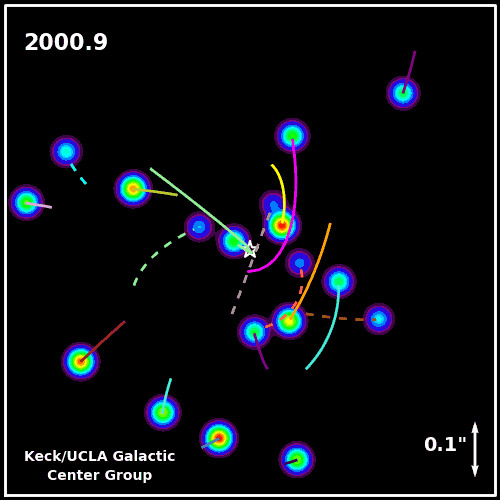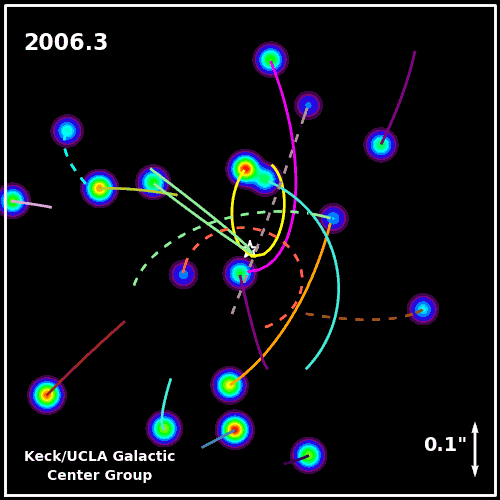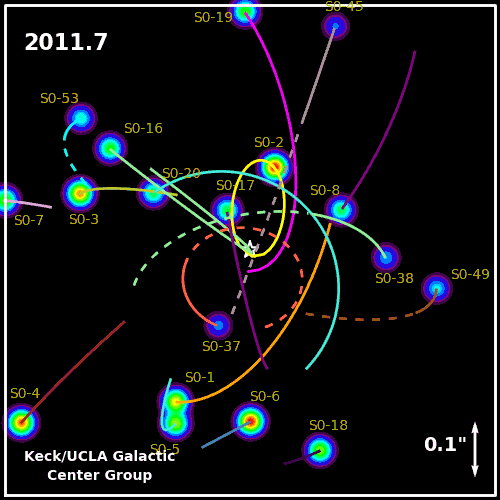
The star S2 is quite remarkable. During its closest pass to Sagitarius A*, S2 travels faster than 5000 km/s! Compare this to the orbital speed of Earth: 29 km/s. This

Laplacian Determinism ↩

Given for one instant an intelligence which could comprehend all the forces by which nature is animated and the respective positions of the beings which compose it, if moreover this intelligence were vast enough to submit these data to analysis, it would embrace in the same formula both the movements of the largest bodies in the universe and those of the lightest atom; to it nothing would be uncertain, and the future as the past would be present to its eyes. Pierre-Simon Laplace

• This is such a satisfying, but rather predictable, viewpoint on the dynamics of the universe. It turned out to be hubris.
• Mathematicians studying Dynamical Systems theory (e.g. Henrí Poincaré) showed there are problems that have intrinsic unpredictability despite being completely deterministic!
• Chaos Theory

Newton’s law of universal gravitation is inconsistent with the constancy of the speed of light ↩

• Thought experiment: Move a distant planet, Newton’s law forecasts instantaneous change of associated gravitational force.
• But experiments have shown that light speed is constant. Nothing propagates faster than the speed of light including the force information indicating that a planet has moved.
• These observations motivated the development of General Relativity by Albert Einstein

Moral: Mathematics has historically been a factory for cleverness. Therefore, you should study it.

Pictures of some mathematicians working today. ↩

* Where will we find mathematicians and other idea developers for the future? *

Advertisement: Toronto Math Circles at the Fields Institute ↩

For your information. There is a meeting of students like you every Saturday at the Fields Institute, 222 College Street, to talk about mathematics at Toronto Math Circles.

Overview

Math Circles is an extracurricular high school enriched-level mathematics club. It has been active in Toronto for several years. While some of the students who attend simply like to work on challenging problems, many others use the weekly circles meetings to help them prepare for mathematics competitions, either individually or as members of a team. Some of the past participants in this program have gone on to represent Canada at the International Mathematical Olympiad, the most elite and prestigious of these competitions.

A generous grant from Angoss Software Corporation will allow some of the participating students to take part in competitions outside of Toronto.

MEETINGS

Mathematics Circles meetings are held at The Fields Institute on Saturday afternoons from 1 PM to 3 PM. The Fields Institute is located at 222 College Street in Toronto.

There are about 50 students participating on a weekly basis.

There will be about fourteen sessions in the fall term (late September to mid December) and about twenty four in the winter spring term, ending by late May or early June.

The Fields Mathematics Circles sessions are open to high school students from throughout the greater Toronto area.

HISTORY

The Math Circles concept was developed in Moscow in the 1950’s as a way to maintain the interest of bright students in mathematics. Challenging material from outside the regular curriculum, as well as preparation for problem solving competitions were seen as the key to maintaining this interest. A critical component to the success of this concept was the active involvement of some of the major figures of the Moscow mathematical community. And, indeed, the Math Circles proved to be highly successful with similar groups established throughout the Soviet Union and beyond. The migration of former Soviet scientists to the West at the end of the twentieth century carried the concept to North America.