Abstract. Many fundamental concepts in mathematics are the results of forgetting something about even more fundamental concepts. Many binomial identities, for example, are the q=1 specializations of even more powerful "q-binomial" identities, whose real home is in some non-commutative universes. Likewise the Euler characteristic of a space is the result of forgetting something about its homology; it is a beautiful and powerful number, but the loss is noticed - homology is a much stronger concept.
Recently it has become clear through the work of Khovanov that many knot invariants, and perhaps many other algebraic objects, are in some sense the Euler characteristics of objects that are potentially much more interesting.
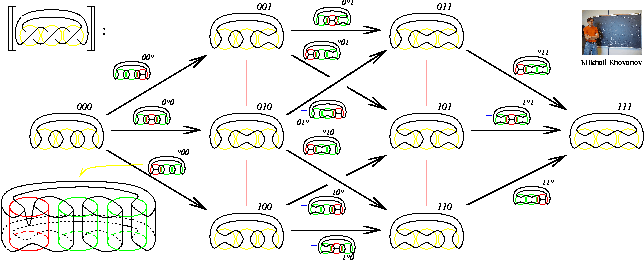
In my talk I will quickly review the easy and elegant Jones polynomial of knots (a "q-object" in itself!). Then I will display one complicated picture and discuss it at length. After some definitions and some intepretation, we will see how it realizes Khovanov's idea in a local manner, leading to some theoretical and computational advantages.
The picture:

Handouts: MoreFormulas.pdf. NewHandout-1.pdf,
Transparencies: Reid2Proof.pdf, R3Full.pdf, T95.html, FrameRack.pdf, KRC.pdf.
See also my paper Khovanov's
Homology for Tangles and Cobordisms.