Khovanov's Categorification of the Jones Polynomial

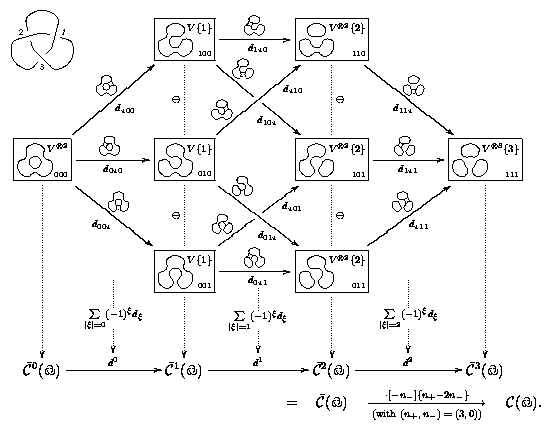
In two recent and very novel papers, arXiv:math.QA/9908171 and arXiv:math.QA/0103190, Khovanov finds a graded chain complex whose graded Euler characteristic is is the Jones polynomial, and proves that each individual homology group of this complex is a link invariant. His construction is very simple and elegant, and yet orthogonal to everything else we know about knot theory and hence extremely interesting. There will be a handout; see the "Quick Reference Guide" for my paper On Khovanov's Categorification of the Jones Polynomial.