





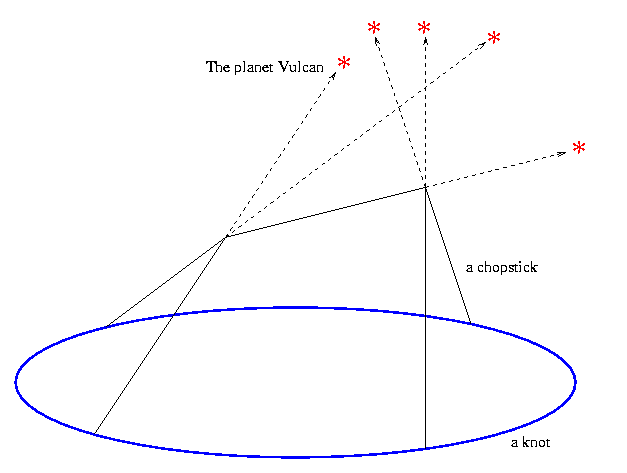
Abstract: It is well known that when the Sun rises on midsummer's morning over the "Heel Stone" at Stonehenge, its first rays shine right through the open arms of the horseshoe arrangement. Thus astrological lineups, one of the pillars of modern thought, are much older than the famed Gaussian linking number of two knots. Recall that the latter is itself an astrological construct: one of the standard ways to compute the Gaussian linking number is to place the two knots in space and then count (with signs) the number of shade points cast on one of the knots by the other knot, with the only lighting coming from some fixed distant star.
Mathematicians can only digest stuff when it is made absolutely general. We therefore pick a knot, given as a specific embedding of S1 in R3, and count the number of all "Stonehenge-inspired chopstick towers" that can be built upon it; namely, the number of delicate arrangements of chopsticks whose ends are lying on the knot or are supporting each other in trivalent corners joining three chopsticks each, so that each chopstick is pointing at a different pre chosen point in heaven that has a high mythical meaning.
Quite amazingly, when these stellar webs are counted correctly, the result is a knot invariant valued in some space of diagrams, deeply related to certain aspects of Lie theory and of the theory of Hopf algebras. We will touch on the former and dwelve into the latter, finding that if the Stonehengians had taken themselves seriously some 4,000 years ago, they would have been forced to discover quasi-Hopf algebras.
This abstract is at http://www.math.toronto.edu/~drorbn/Talks/Lehigh-0006/.
Handout:

|
|
handout.pdf |
| Side 1 (talk summary). | Side 2 (IHX, riddle, credits). | Both sides at higher resolution (1049Kb). |