Colloquium, February 17.
Abstract. Over the last 20 years, knot theorists have been extremely good at borrowing ideas from other fields. We've borrowed from Mathematical Physics and borrowed from Algebra and we have a Beautiful Theory of Knot Invariants that can claim deep heritage on either side. But we haven't been so good at returning. While not entirely impossible, is remains difficult to point at developments in quantum field theory or quantum algebra (our lenders) that owe something to our Beautiful Theory of Knot Invariants.
Came Khovanov in 1999 and changed the picture dramatically by offering Mathematical Physics and Algebra the most valuable prize known to mathematicians - a challenge. For none of them can yet explain whence comes his "Categorification of the Jones Polynomial" - a far reaching generalization of the most celebrated member of our Beautiful Theory of Knot Invariants. The Mathematical Physics and Algebra underlying the Jones polynomial are deep and substantial, and there are all reasons to believe that a successful resolution of Khovanov's challenge will be the same.
In my talk I will quickly describe the Jones polynomial (it's so easy) and then move on to describe Khovanov's homological generalization thereof.
(Khovanov's homology is also a stronger invariant than the Jones polynomial and it is "functorial" in some 4-dimensional sense).
Handout: QRG.pdf.
Slide: Kauffman's
Bracket.
Seminar, February 18.
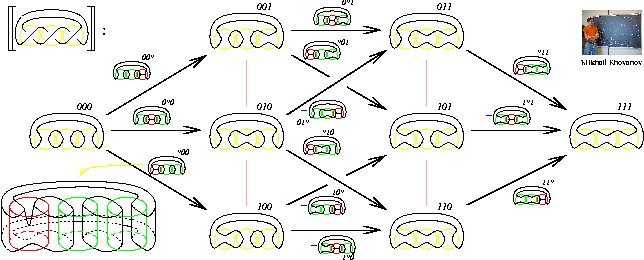
Abstract. In my talk I will display one complicated picture and discuss it at length. Applying a certain 2D TQFT, we will get a homology theory whose Euler characteristic is the Jones polynomial. Not applying it, very cheaply we will get an invariant of tangles which is functorial under cobordisms and an invariant of 2-knots.
Handout side 1:
NewHandout-1.pdf.
Handout side 2:
handout2.pdf.
The Picture:
