Abstract. Khovanov homology is a homology theory whose Euler characteristic is the (by now classical) Jones polynomial. It is a finer invariant yet it remains computable. It is functorial in the appropriate sense and hence it is more geometric, and thus it is already responsible for some new topological results and some major simplifications of less new ones. But that's not why it is really exciting; to find that out, you'll have to come to my talk.
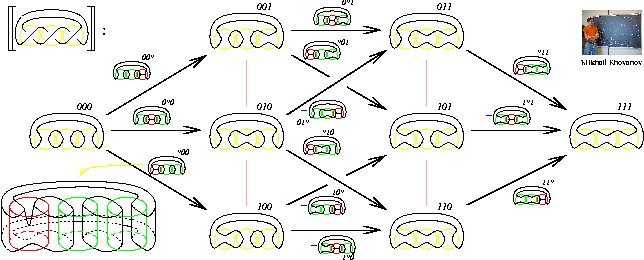
My talk will be centered around one picture, shown below, and will follow two handouts, posted here.
The picture:

Handouts:
KhovanovOverview-1.pdf,
KhovanovOverview-2.pdf.
Transparency:
R3Full.pdf.
See also my paper Khovanov's
Homology for Tangles and Cobordisms.