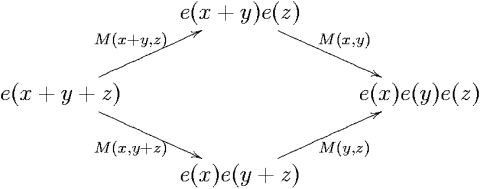
Abstract. Often in mathematics one needs to solve certain non-linear functional equations and sometimes one can be helped by certain techniques from homological algebra. After quickly mentioning a few typical examples for that need I will concentrate on the simplest example I'm aware of - finding a solution e of the non-linear functional equation e(x+y)=e(x)e(y) within the algebra Q[[x]] of power series in the variable x with rational coefficients. The point of course is the technique, not the actual solution, which I'm sure you all know well.
It is worth noting that in some a priori sense the existence a solution of e(x+y)=e(x)e(y) is unexpected. For e must be an element of the relatively small space Q[[x]] of power series in one variable, but the equation it is required to satisfy lives in the much bigger space Q[[x,y]] of power series in two variables. Thus in some sense we have more equations than unknowns and a solution is unlikely. How fortunate we are that exponentials do exist, after all!

Also see my paperlet The Existence of the Exponential Function (with contributions by Omar Antolin Camarena).