Navigation Panel: (IMAGE)(IMAGE)(IMAGE)(IMAGE) (SWITCH TO TEXT-ONLY VERSION) (IMAGE)(IMAGE) (These buttons explained below)
UNIVERSITY OF TORONTO MATHEMATICS NETWORK

Answers and Explanations

The Number e as a Limit

So far we've talked about "continually compounding" interest: interest is assumed to be earned continually. In many bank accounts, however, interest only starts becoming eligible to earn further interest on specific dates (such as the end of each month, or the end of each year) when it is officially added in to your balance. The calculation of compound interest is different in this case, and this different calculation gives a nice mathematical definition of the number e.

Suppose the simple interest rate is 100% for a certain period. Under simple interest alone, the money will double during that period. Under continually compounding interest, it will be multiplied by e. But what happens if interest is compounded at n equally spaced dates during that period (such as at the and of each month), rather than continually?

In the interval before the first compounding date, you are just earning simple interest on the original balance. Let's call the original balance B. The interest rate for this interval is 1/n, since the total interest rate for all n intervals is 1 (100% is just another way of writing 1). So, on the first compounding date, one gets paid interest in the amount of (1/n)B. The balance after this payment is therefore B + (1/n)B which equals (1 + (1/n)) B. In other words:

(balance at end of first interval) = (1 + (1/n)) times (balance at start of first interval)
  = (1 + (1/n)) B.
During the second interval (between the first and second compounding dates), one is again earning interest at a rate of 1/n, but this time on this new balance (1 + (1/n))B. Therefore,
(balance at end of second interval) = (1 + (1/n)) times (balance at start of second interval)
  = (1 + (1/n)) times (1 + (1/n)) B
  = (IMAGE) .
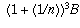If you do this same calculation again, you find that the balance at the end of the third interval is (IMAGE) and so on. The balance at the end of the nth and final interval is (IMAGE) .

Therefore: if the interest is compounded n times during the period, the final balance is 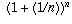(IMAGE) times the original balance.

Compounding at more and more frequent intervals means that one is approximating more and more closely the idea of continual compounding which we talked about earlier, in which the final balance is e times the original balance. What this means is that

The number e is the limit of the quantity 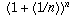(IMAGE) as n goes to infinity.

This gives a nice mathematical definition of the number e.

[Go On]

This page last updated: September 1, 1997
Original Web Site Creator / Mathematical Content Developer: Philip Spencer
Current Network Coordinator and Contact Person: Any Wilk - mathnet@math.toronto.edu

Navigation Panel: (IMAGE)(IMAGE)(IMAGE)(IMAGE) (SWITCH TO TEXT-ONLY VERSION) (IMAGE)(IMAGE)

(IMAGE) Go backward to The General Situation
(IMAGE) Go up to Does the Number e Have Special Meaning?
(IMAGE) Go forward to The Number e in Calculus
(SWITCH TO TEXT-ONLY VERSION) Switch to text-only version (no graphics)
(IMAGE) Access printed version in PostScript format (requires PostScript printer)
(IMAGE) Go to University of Toronto Mathematics Network Home Page