Question Corner and Discussion Area
Question Corner and Discussion Area
I want to know how to construct a pentagon. I have done it before, but I have forgotten how. I remember it is similar to constructing a hexagon, but a bit more difficult. Thanks.There are several ways to do it. Unfortunately we are very short-staffed right now and cannot spare the resources to hunt down the easiest and most elegant construction. However, the following method will work:
Constructing a pentagon is equivalent to dividing a circle (a full 360
degrees) up into five equal parts (angle 72 degrees each). The cosine of
72 degrees is 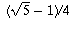 (this can be found by starting with the
equation
(this can be found by starting with the
equation 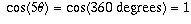 ,
using trigonometric identities to write
,
using trigonometric identities to write 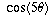 as a polynomial
in
as a polynomial
in 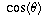 , factoring and solving the resulting polynomial equation
for
, factoring and solving the resulting polynomial equation
for 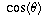 ).
).
Therefore, this angle of 72 degrees can be constructed by building a
right-angled triangle whose hypotenuse is 4 and whose adjacent side is
of length 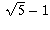 . This latter length can be constructed by taking
hypotenuse of a right triangle whose other sides have lengths 1 and 2,
and subtracting length 1 from it.
. This latter length can be constructed by taking
hypotenuse of a right triangle whose other sides have lengths 1 and 2,
and subtracting length 1 from it.
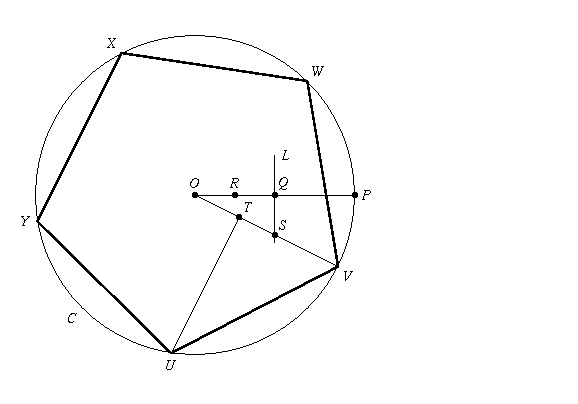
The following procedure uses this idea to construct a pentagon:
Start with a circle C, with centre point O. Let P be a point on C. Draw the perpendicular bisector L to segment OP (bisecting it at point Q). Construct the midpoint R of OQ. (RQ is going to be our unit length).
With centre Q and radius RQ, draw an arc intersecting L at point
S. Draw segment OS.
(This is the hypotenuse of a right triangle OQS whose other sides have
length 1 and 2, so OS has length 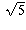 ).
).
With centre S and radius RQ (= QS), draw an arc intersecting OS at point
T. (Now OT has length 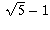 ).
).
Construct the line passing through point T at right angles to OT. Let it intersect the circle C at point U.
Now the triangle OTU has hypotenuse of length OU = radius of C = 4,
and side length 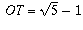 . Therefore, angle UOT is 72 degrees.
Extend segment OT past S until it meets the circle C at point V;
you have now constructed two vertices (U and V) of the pentagon.
. Therefore, angle UOT is 72 degrees.
Extend segment OT past S until it meets the circle C at point V;
you have now constructed two vertices (U and V) of the pentagon.
To construct the remaining vertices: with centre V and radius UV draw an arc intersecting C at point W. With centre W and the same radius, draw an arc intersecting C at point X. Finally, with centre X and the same radius, draw an arc intersecting C at point Y. UVWXY will be a pentagon.
There are probably much more efficient ways to do it, but the above procedure will certainly work, for the reasons described. The procedure is illustrated below:
![]() Go backward to Do Parallel Lines Meet At Infinity?
Go backward to Do Parallel Lines Meet At Infinity?![]() Go up to Question Corner Index
Go up to Question Corner Index![]() Go forward to The Three Classical Impossible Constructions of Geometry
Go forward to The Three Classical Impossible Constructions of Geometry![]() Switch to text-only version (no graphics)
Switch to text-only version (no graphics)![]() Access printed version in PostScript format (requires PostScript printer)
Access printed version in PostScript format (requires PostScript printer)![]() Go to University of Toronto Mathematics Network
Home Page
Go to University of Toronto Mathematics Network
Home Page