MULTIVARIABLE CALCULUS

COURSE 2005-2006

SAMPLES OF PREVIOUS YEAR'S TESTS

TEST #1. COURSE 2003-2004.

1.  Consider the vectors  a = j - k ,  b = 2 i - 2  j + k ,  c = i + 4 j - 3 k ,  and  d = i + 2  j .

a) (5 marks) Find the angle between the vectors  a  and  b .

b) (5 marks) Find the area of the parallelogram spanned by the vectors  c  and  d .

c) (5 marks) Find the volume of the parallelepiped spanned by the vectors  a ,  b , and  c .

2. a) (5 marks) Consider the surface described by the equation  ( 1 + ( x – y ) ² ) z = x ( 5 – 2 y z )  in Cartesian  coordinates. Find an equation of the form  z = f ( r , q )  to describe this surface using cylindrical coordinates. Find the value of  z  when  r = 2  and  q = p / 3 .    

b) (5 marks) Consider the surface described by the equation  x ² + ( y – 1 ) ² + 2 z ² = 1  in Cartesian  coordinates. Find an equation of the form  r  = g (q , f )  to describe this surface using spherical coordinates.  Find the value of  r  when  q = p / 3  and  f =  p / 2 .

3. (15 marks) Let  S  be the surface described by the equation  2 ( x  ³ + y  ³ – z  ³ ) – ( x + y – z )  ³ = – 4  .

Let  l  be the line that is normal to the surface  S  at the point  ( 1 , 0 , – 1 )  and let  p  be the plane that is tangent to the surface  S  at the point  ( 1 , 1 , 0 ) . Find the coordinates of the point of intersection of the line  l  and the plane  p .

4. a) (5 marks) State, without proof, the Triangle Inequality and the Cauchy-Schwarz Inequality for any vectors  v  and  w  in  ⁿ .

b) (5 marks) Use both, the Triangle Inequality and the Cauchy-Schwarz Inequality, to show that the inequality    holds for any three vectors  a ,  b , and  c  in  ⁿ .

5. a) (5 marks) Is the set  A = { ( x , y ) Î ² ½ y ¹ 0 }  an open set? Briefly explain.

b) (5 marks) Evaluate   or briefly explain why this limit does not exist.

c) (5 marks) Let  .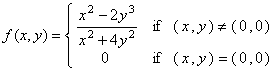

Compute   or briefly explain why this partial derivative does not exist.

d) (5 marks) Let  f : ² ® ²  and  g : ² ® ²  be differentiable functions, such that  f ( 4 , 5 ) = ( 6 , 7 ) ,

D f ( 4 , 5 ) =  , and  D g ( 6 , 7 ) =  . Compute  D ( g o f ) ( 4 , 5 ) .

6. (10 marks) Let  w = x ³ + y ³ , where  x = 2 s + 3 t  and  y = 3 s + 2 t .

Show that 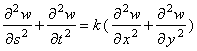   and find the value of the constant  k . 

7. Let  f : ² ®   be a function whose first and second order partial derivatives are continuous. Suppose that:   f ( 0 , 1 ) = 5 ,  ,  ,  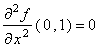,   , and   .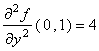

a) (10 marks) Determine the second-order Taylor formula for the function  f  at the point  ( 0 , 1 )  and use it   to find an approximated value for  f ( 0.2 , 0.9 ) .

b) (10 marks) Let  u Î ²  denote a unit vector. Let  g ( x , y )  denote the directional derivative of the function  f ( x , y )  along the vector  u  and let  h ( x , y )  denote the directional derivative of the function  g ( x , y )  along the vector  u . Find all unit vectors  u , if any, for which  h ( 0 , 1 ) = 0 . (Hint: Represent the unit vector as  u = ( u ₁ , u ₂ ) , express  h ( x , y )  in terms of  u ₁ ,  u ₂ , 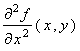 ,    and 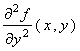  , then obtain  h ( 0 , 1 )  in terms of  u ₁  and  u ₂ .)