| © | Dror Bar-Natan: Classes: 2014-15: Math 475 - Problem Solving Seminar: | (22) |
Next: Blackboards for Thursday February 5
Previous: Blackboards for Tuesday February 3 |
Reading. Sections 1.5 and 1.6 of Larson's textbook.
Next Quiz. Thursday February 12, on these two sections.

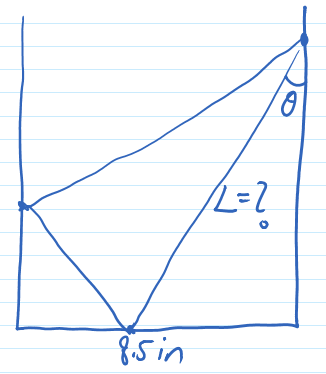
Problem 1 (Larson's 1.5.7). The bottom of this handout (width 8.5in) is folded up and to the left, so that the bottom right corner would align with the left edge of this page. Given the angle of the fold $\theta$, what is the length of the crease $L$? See the figure on the right.
Problem 2 (Larson's 1.5.8). Let $P_1,P_2,\ldots,P_{12}$ be the vertices of a regular 12-gon. Are the diagonals $P_1P_9$, $P_2P_{11}$ and $P_4P_{12}$ concurrent?
Problem 3 (Larson's 1.5.2).
Dror's Favourite "Choose an Effective Notation" problem is more a computer problem than a math problem, yet it is pretty and it will make us look at some pretty (and significant!) mathematics.
The Kauffman Bracket $\langle D\rangle$ of a knot diagram $D$
is defined by the following recursive relations:

Remark. The celebrated "Jones Polynomial" of $D$ is very easily defined from $\langle D\rangle$, \[ J(D) = \left.(-A^3)^{w(D)}\frac{\langle D\rangle}{-A^2-A^{-2}}\right|_{A\to q^{1/4}}, \] where $w(D)$ is the writhe of $D$, the difference between the number of right-handed and left-handed crossings in $D$. Yet this matters not for us today.
Homework Problem (not to be submitted, yet fame for an
excellent solution). Write a very short computer program that will be
able to compute the Kauffman bracket (and hence the Jones polynomial)
of the following three knots:

Problem 4 (Larson's 1.6.2).
Problem 5 (Larson's 1.6.4). Let $P$ be a point on the graph $G$ of $y=f(x)$, where $f$ is a cubic polynomial. Assume the tangent to the curve at $P$ intersects $G$ again at a point $Q$. Let $A$ be the area bound by $G$ and the segment $PQ$, and let $B$ be the area defined in exactly the same manner, except starting with $Q$ rather than with $P$. What is the relationship between $A$ and $B$?
Problem 6. A function on the plane has the property that the sum of its values on the corners of any square (of any size and orientation) is zero. Prove that the function is the zero function.
Problem 7. Prove: You cannot colour the points of the plane with just three colours, so that no two points of distance 1 will be coloured with the same colour. What if you had four colours available?
Dror's Favourite "Exploit Symmetry" problem: Two players alternate placing $1\times 1$, $2\times 1$, and $4\times 1$ lego pieces on a circular table of diameter 100, with no overlaps. If a player cannot place a further piece, (s)he looses. Would you rather be the first to move of the second?
Dror's Favourite "Explore Symmetry" topic: See http://drorbn.net/Treehouse:
