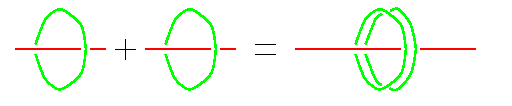
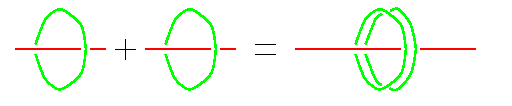
One of the earliest demonstrations of the identity 1+1=2 was using the Chinese soroban (abacus). The proof is topological in nature: the number 1 is represented by a rod with a bead on it. The sum 1+1 would be taking two such rods and connecting them end to end, and the result is clearly topologically equivalent to the number 2, represented by a single rod with a double bead on it. In modern language, a "rod with a bead" is nothing but the Hopf link, with one of the components cut open, and the identity 1+1=2 becomes "the connected sum of two cut Hopf Links is equal to a single cut Hopf Link, with its uncut component doubled".
In our lecture we will explain how, via the Kontsevich integral and a certain diagrammatic calculus, the equality 1+1=2 implies that certain two big sums of diagrams are equal (modulo some necessary relations). When a Lie algebra is given and these diagrams are interpreted as tensors in certain spaces associated with the Lie algebra, this equality becomes an easy proof of the multiplicative property of the non-obvious Harish-Chandra-Duflo isomorphism.
The diagram equality we prove and use is the "Wheeling Conjecture" of Garoufalidis, Rozansky, D. Thurston and myself (1995), and, independently, of Deligne (1996). The 1+1=2 proof is due to Le, D. Thurston and myself (1998). The Wheeling Theorem was recently used by Hitchin and Sawon (math/9908114) to give a formula for the L2 norm of the curvature of an irreducible hyperkahler manifold in terms of the volume and Pontryagin numbers, and (using also Wheeling's sister theorem, the Wheels theorem) by Lawrence and myself (in preparation) to compute the Kontsevich integral and the LMO invariant of a certain class of links and 3-manifolds.