© | << < ? > >> |
Dror Bar-Natan:
Talks:
Khovanov Homology for Tangles and Cobordisms
Colloquium, University of Toronto
SS5017, 4PM, December 8, 2004
Abstract. In my talk I will display one complicated picture
and discuss it at length, finding that it's actually quite simple.
Applying a certain 2D TQFT, we will get a homology theory whose Euler
characteristic is the Jones polynomial. Not applying it, very cheaply
we will get an invariant of tangles which is functorial under
cobordisms and an invariant of 2-knots.
Why is it interesting?
- It has several generalizations, but as a whole, we hardly understand
it. It may have significant algebraic and/or physical ramifications. In
fact, it suggests that much of algebra as we know it (or at least quantum
algebra as we know it), is a shadow of some "higher algebra".
- It is a knot/link/tangle invariant stronger than the Jones polynomial,
and an invariant of 2-knots in 4-space.
- It seems stronger than the original "Khovanov Homology", which in
itself is stronger than the Jones polynomial.
- It is functorial in the appropriate sense, and Rasmussen (math.GT/0402131)
uses it to do some real topology.
Prerequisites. Not to be scared of the words "category" and
"functor" and the phrase "a homotopy between chain complexes".
Otherwise all will be explained.
The picture:
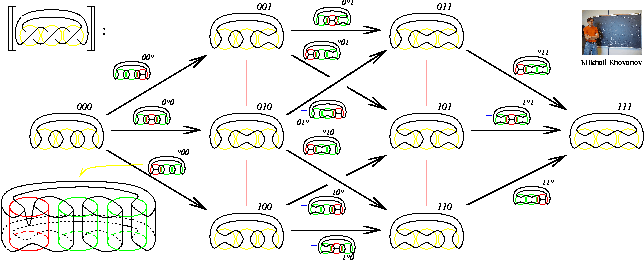
Handouts:
MoreFormulas.pdf.
NewHandout-1.pdf,
Transparencies:
Reid2Proof.pdf,
R3Full.pdf,
FrameRack.pdf.
See also my paper Khovanov's
Homology for Tangles and Cobordisms.

