Summary. A brief introduction to the fundamental theorem and universal finite type invariants. You can find all that (and more) in [BNS].

The Fundamental Theorem of Finite Type Invariants1 has a deceptively simple formulation and a surprising number of proofs and partial proofs, each one coming with its own philosophy and employing its own set of tools. The purpose of this article is to further study one family of approaches, the algebraic approaches, not so much as to prove the theorem, for this summit is already multiply climbed, but rather for the mere beauty of these specific paths, for the view from some of the vista points along those, for some new perspectives and insights gained along the way, and, well, o.k., also for an occassional technical advantage over the other approaches. In fact, some of the paths we will take don't even make it all the way to the top, or if they do, they are sometimes obviously non-geodetic, but to find the nearby shorter routes one would have to venture a bit into still unexplored territory. So another reason for the existance of this article is to encourage ourselves, and others, to complete and improve what we already have. Thus quoting from the abstract, this article suggests many ``live ends'', unfinished problems that don't seem to be dead ends.
In one form, the Fundamental Theorem of Finite Type Invariants, or just
the Fundamental Theorem throughout this article, asserts that there
exists a universal finite type invariant, an essential invariant
![]() . Let us start by defining the terms
in this statement, and then, in the further parts of this introduction,
we will sketch the algebraic family of approaches (to be followed by
full details in Sections 2-4):
. Let us start by defining the terms
in this statement, and then, in the further parts of this introduction,
we will sketch the algebraic family of approaches (to be followed by
full details in Sections 2-4):
![]()
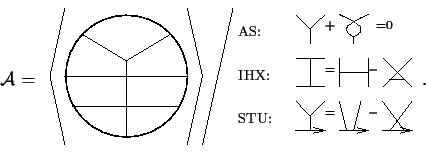
An equivalent formulation of the Fundamental Theorem is that every
degree ![]() weight system is the
weight system is the ![]() th derivative of some type
th derivative of some type ![]() invariant; in particular, it follows that there are lots of finite type
invariants, and it reduces the problem of their enumeration to a finite
algebro-combinatorial problem at any fixed degree.
invariant; in particular, it follows that there are lots of finite type
invariants, and it reduces the problem of their enumeration to a finite
algebro-combinatorial problem at any fixed degree.