Navigation Panel: (IMAGE)(IMAGE)(IMAGE)(IMAGE) (SWITCH TO TEXT-ONLY VERSION) (IMAGE)(IMAGE) (These buttons explained below)
UNIVERSITY OF TORONTO MATHEMATICS NETWORK

International Mathematical Talent Search

Round 17

Problem 1/17. The 154-digit number, 19202122. . . 939495, was obtained by listing the integers from 19 to 95 in succession. We are to remove 95 of its digits, so that the resulting number is as large as possible. What are the first 19 digits of this 59-digit number?

Problem 2/17. Find all pairs of positive integers (m,n) for which 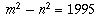(IMAGE) .

Problem 3/17. Show that it is possible to arrange in the plane 8 points so that no 5 of them will be the vertices of a convex pentagon. (A polygon is convex if all of its interior angles are less than or equal to 180 degrees).

Problem 4/17. A man is 6 years older than his wife. He noticed 4 years ago that he has been married to her exactly half of his life. How old will he be on their 50th anniversary if in 10 years she will have spent two-thirds of her life married to him?

Problem 5/17. What is the minimum number of 3 by 5 rectangles that will cover a 26 by 26 square? The rectangles may overlap each other and/or the edges of the square. You should demonstrate your conclusion with a sketch of the covering.

Solve as many of the problems as you can (you need not solve them all), and mail your solutions to:

Professor E. J. Barbeau
Department of Mathematics
University of Toronto
Toronto, ON M5S 3G3
Make sure that the front page of your solutions contains your full name and mailing address.
These problems are made available through the quarterly journal Mathematics and Informatics. Student subscriptions at US$12 (student rate) or US$18 (teacher rate) may be ordered from Prof. George Berzsenyi, Department of Mathematics, Box 121, Rose-Hulman Institute of Technology, Terre Haute, IN 47803-3999, U.S.A. Remittances should be payable to Mathematics and Informatics.
This page last updated: February 3, 1997
Original Web Site Creator / Mathematical Content Developer: Philip Spencer
Current Network Coordinator and Contact Person: Joel Chan - mathnet@math.toronto.edu

Navigation Panel: (IMAGE)(IMAGE)(IMAGE)(IMAGE) (SWITCH TO TEXT-ONLY VERSION) (IMAGE)(IMAGE)

(IMAGE) Go backward to Round 16
(IMAGE) Go up to Talent Search Index
(IMAGE) Go forward to Round 18
(SWITCH TO TEXT-ONLY VERSION) Switch to text-only version (no graphics)
(IMAGE) Access printed version in PostScript format (requires PostScript printer)
(IMAGE) Go to University of Toronto Mathematics Network Home Page